donotturnoff

The Lorenz System is a system of differential equations which was discovered by Edward Lorenz as a part of his research into mathematical models of the weather. It is a simplified model of convection which plots the rate of convection along the x axis and the horizontal and vertical temperature variation along the y and z axes respectively.

It is defined by the following equations:

• dx⁄dt = σ(y - x)
• dy⁄dt = x(ρ - z) - y
• dz⁄dt = xy - βz

σ, ρ and β are certain physical parameters of the system, which are usually given the values σ=10, ρ=28 and β=8⁄3. These values (and other nearby values) make the system exhibit chaotic behaviour. Other values may make the system change periodically, or chaotically.

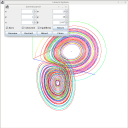
The system produces beautiful patterns, often with two connected round "tracks", with the appearance of a butterfly's wings (or kind of like Saturn's rings, but not just rings).

I watched this video in late 2018 and decided it'd be fun to try to make my own Lorenz system visualiser. I had recently built a 3D rendering engine and thought it'd be a good test of its capabilities, so I set about making a simple orientable Lorenz system.

Screenshots

A Lorenz system being plotted

Dependencies

• JThree

To do

There are a couple of rendering bugs but they are due to the underlying rendering engine, which I probably won't be working on any more.